From the jungle of stochastic optimization to… Sequential Decision Analytics

I send out frequent updates regarding my work on LinkedIn – if you are not a follower, please reach out and ask to join.

Some highlights:

• New! I have created a webpage summarizing a field that I am calling “sequential decision analytics”.  See the video introduction to sequential decision analytics.
• For an introduction to the unified framework: I revised and re-recorded a tutorial on the unified framework that I gave at the Kellogg School of Business at Northwestern (February 2020).  It is now on YouTube in two parts:
  • Part I – Describes applications, the universal modeling framework, and introduces the four classes of policies for making decisions in the context of pure learning problems (derivative free stochastic search, also known as bandit problems). Slides to Part I.
  • Part II – Here I illustrate the four classes of policies in the context of more general state-dependent problems.  I then briefly illustrate how these ideas are used at Optimal Dynamics. Slides to Part II.
• Scroll down to “Educational materials” for more material.

• Scroll down to “Talks and videos” for other presentations. 

Sequential decision problems are problems that consist of decision, information, decision, information, …. while incurring costs or receiving rewards.  Sequential decision problems cover an incredibly broad problem class, spanning engineering, the sciences, business, economics, finance, health, transportation, energy and e-commerce.   The problems may be discrete dynamic programs, continuous control problems, graph problems, stochastic search, active learning, and multiagent games and applications. 

We have a very good handle on modeling deterministic optimization problems, but the universe of problems that involve sequential decisions and information have resisted being expressed in the kind of common canonical framework that has become universal in deterministic optimization.

Sequential decision problems are so diverse that the field has become fragmented into a Balkanized set of communities with competing algorithmic strategies and modeling styles. It is easy to spend a significant part of a career mastering the subtleties of each perspective on stochastic optimization, without recognizing the common themes.

We have developed a unified framework that covers all of these communities. We break all sequential decision problems into five components: state variables, decision variables, exogenous information variables, the transition function, and the objective function. We search over policies, which are functions (or methods) for making decisions. We have identified two core strategies for designing policies (policy search, and policies based on lookahead approximations), each of which further divides into two subclasses, creating four classes that cover all of the solution approaches in the books illustrated above, as well as anything being used in practice.

The modeling and algorithmic challenges involve three core elements:

• Modeling the problem (state variables, decision variables, exogenous information processes, transition function, objective function).
• Modeling the uncertainty (uncertainty quantification).
• Designing and evaluating policies.

There is a growing community, which started in computer science, which uses the term “reinforcement learning” to refer to sequential decision problems.  My explanation of “artificial intelligence,” “machine learning,” and “reinforcement learning.”

Our approach does not replace any prior work: rather, it brings all of this work together, and helps to identify opportunities for cross-fertilization.  A good way to think of the unified framework is “standing on the shoulders of giants.”

Educational materials:

All of the material below, including the material for the graduate course, is written for students with an undergraduate course in probability and statistics.  From time to time a second course in probability may be useful, and I occasionally present problems that use linear programming, but in a way that can be read without a full course in math programming (there may be occasional exceptions).  

• • W.B. Powell,  “From Reinforcement Learning to Optimal Control: A unified framework for sequential decisions” – This describes the frameworks of reinforcement learning and optimal control, and compares both to my unified framework (hint: very close to that used by optimal control).  The modeling framework and four classes of policies are illustrated using energy storage.
    
  • W.B. Powell, A unified framework for stochastic optimization, European Journal of Operational Research, Vol. 275, No. 3, pp. 795-821 (2019). – An invited review article to appear in European J. Operational Research. This is my latest attempt to pull this field together in a 25 page tutorial.
  • Energy storage research – This is a web page summarizing two dozen papers on a variety of energy storage problems.  The webpage provides thumbnail sketches of each research project, with links to the paper (and some software).  I u se all four classes of policies, and one project was the inspiration for what I now call “backward approximate dynamic programming.”  
  • “On State Variables, Bandit Problems and POMDPs” – A thought piece on modeling active learning problems, using flu mitigation as an illustrative examples.  This was written just before the COVID pandemic, but has ideas that are very relevant.
  • I teach this material in an undergraduate course at Princeton: ORF 411 – Sequential Decision Analytics and Modeling. Below are some materials from the course:
    • ORF411 Course Web Page, with a complete set of lecture notes in PowerPoint.
    • There is an online textbook for the course at Sequential Decision Analytics and Modeling course notes. Cite this reference as: Warren B. Powell, Sequential Decision Analytics and Modeling, Department of Operations Research and Financial Engineering, Princeton University, 2019.
    • You are invited to contribute chapters to the book via an editable version.
    • Python modules that accompany “Sequential Decision Analytics and Modeling.” – There is a python module for most of the chapters.  Most of these have been used in an undergraduate course at Princeton.
  • There is also a graduate level course that I taught at Princeton: ORF 544 –  Stochastic Optimization and Learning. Additional materials are:
    • • The webpage for the ORF 544 course, complete with all lecture notes in PowerPoint.
    • A book (in progress) written entirely around this framework can be accessed at Reinforcement Learning and Stochastic Optimization: A unified framework for sequential decisions  (this is being continually updated) – This is a book (in progress ~700 pages) that is designed entirely around the unified framework. This book is used in a graduate course on stochastic optimization.  Cite this reference as: Warren B. Powell, Reinforcement Learning and Stochastic Optimization and Learning: A Unified Framework, Department of Operations Research and Financial Engineering, Princeton University, 2019. 
  • A very short presentation illustrating the jungle of stochastic optimization (updated April 12, 2019).  The last slide shows the evolution of seven major communities from their origin using one of the four classes of policies, to where they stand now (using two, three or often all four classes of policies.

Talks and videos:

• • I am now posting videos on youtube under the channel for Optimal Dynamics.
  • Youtube video of talk given for REFASHIOND Ventures on sequential decision analytics, with examples from supply chain management.
  • 90 minute presentation at Northwestern Kellogg School of Business, Feb 19, 2020.  This is my latest “unified framework” talk.  For the first time, I illustrated the four classes of policies using two broad problem classes: pure learning problems (“state-independent problems”) and the more complex “state-dependent problems.” A video of the talk.
  • I gave a 2-day workshop on the unified framework at the Olin Business School at Washington University in St. Louis Nov 5-6, 2019.  2-day workshop Syllabus. The powerpoint slides are below:
    • 1. Introduction
    • 2. Modeling, state variables
    • 3. Modeling energy storage, uncertainty
    • 4. Designing policies
    • 5. Belief models, sequential learning
    • 6. Active learning
    • 7. Policies for active learning
    • 8. Policy search (derivative-based and derivative-free)
    • 9. Mixed learning-resource allocation
    • 10. High dimensional ADP for resource allocation
    • 11. Stochastic lookahead policies
    • 12. Supply chain management
    • 13. The modeling process
    • 14. Guidelines for choosing policies
    • 15. Reading materials

  • My 90 minute tutorial at Informs  (powerpoint) (pdf).  The recording I made of my INFORMS talk.  If you attended the talk, please provide feedback here

• See the list of past and pending talks.  If you are interested in me giving a talk at your school or company, send me an email.

Some key points

• State variables – We claim that all properly modeled dynamic systems are Markovian, and provide a teachable, implementable definition that students can use to guide their efforts to model these systems (see chapter 9 in Reinforcement Learning and Stochastic Optimization available at link above). (If you have a counterexample, email it to me). But examine this for a fresh perspective on state variables.
• A dynamic program is a sequential decision problem (it is not a method). Bellman’s equations are a) conditions for an optimal policy and b) a path to designing good policies (but just one of four paths).  
• We introduce the distinction between the base model, which is our model of the problem we are trying to solve, and a lookahead model, widely used as one class of policy (especially in stochastic programming). The base model is often referred to as a “simulator” without recognizing that this is the problem we are trying to solve. The base model is comparable to the objective function in a deterministic optimization model.
• When solving a deterministic optimization problem, we want to find the best decision (often a real-valued vector). When solving a stochastic optimization problem, we typically want to find the best function (known as a policy). 
• A multistage stochastic program (using scenario trees) is a lookahead model for designing a policy (called a lookahead policy) for solving dynamic programs. An optimal solution of a lookahead model is generally not an optimal policy (even if it is hard to solve).
• “Robust optimization” (for sequential problems) is a lookahead policy (using a min-max objective) to solve a dynamic program where the objective may be formulated using an expectation (which is what is implied if you simulate the policy and average the results), or the worst case (which is consistent with the robust concept) or any other risk measure.

Our canonical model

The slides below provide a thumbnail sketch of the central idea behind our modeling and algorithmic strategy.

The first slide below contrasts the standard canonical form for a multiperiod, deterministic linear program (on the left), and the approach we are advocating to be the canonical form for a sequential, stochastic optimization problem:

The key idea is that when working on sequential stochastic problems, you are searching for the best function (known as a policy), rather than the more familiar problem of finding the best real-valued scalar or vector.

This raises the obvious question – how do you search over a space of functions???

We have taken a practical path for solving this question. We have identified four fundamental (meta) classes of policies, called PFAs, CFAs, VFAs and DLAs (direct lookaheads). These are summarized on the following slide:

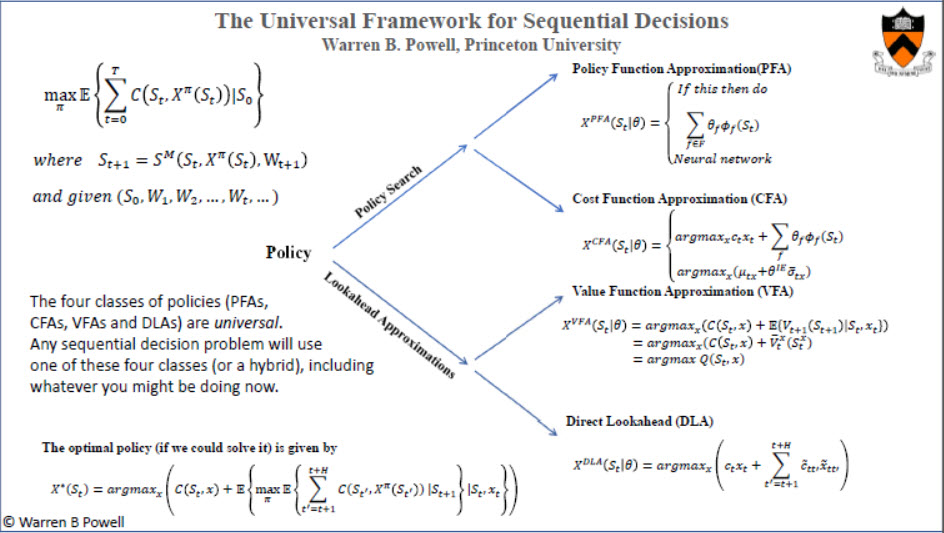
We let \pi be the variable that captures both the type of function, and any parameters that determine the behavior of the function. A tunable parameter could be a regression parameter, or variables that determine the planning horizon, number of stages and number of scenarios.

In the equations above, we use tildes on variables that describe the lookahead model to avoid confusing them with the base model. This is only an issue when we are using lookahead policies.

Note that these four classes of policies span all the standard modeling and algorithmic paradigms, including dynamic programming (including approximate/adaptive dynamic programming and reinforcement learning), stochastic programming, and optimal control (including model predictive control).

It is important to recognize that even for the same problem, each of the four classes of policies may work best, depending on the data. We demonstrate this in the context of a simple energy storage problem. We created five problems, which we solved using each of the four classes of policies, plus a hybrid. In the graph below, we report the performance of each policy as a fraction of the posterior optimal (the best you could do with perfect information). Each policy works best on one of the five problems.

W.B. Powell, S. Meisel, Tutorial on Stochastic Optimization in Energy II: An energy storage illustration, IEEE Trans. on Power Systems, Vol. 31, No. 2, pp. 1468-1475, 2016

We prefer the approach universally used in deterministic optimization where we formulate the problem first, and then we design methods to find a solution (in the form of a policy). But this requires accepting that in sequential problems, we are not looking for decisions (as we do in deterministic models), but rather functions (or policies). Classical strategies in stochastic optimization (which are described using familiar labels such as dynamic programming, stochastic programming, robust optimization and optimal control) actually represent particular classes of policies. So, to solve a problem using one of these approaches means you are actually choosing the class of policy before you have even started modeling the problem.

Warren Powell
wbpowell328@gmail.com