Warren B. Powell, Professor Emeritus, Princeton University
wbpowell328@gmail.com
I spent a career working on a wide range of problems that involve making decisions
over time, as new information is arriving. This problem class arises in virtually any human activity spanning science and engineering, energy, economics and finance, health, business and the social sciences. I refer to these as sequential decision problems which has attracted the attention of at least 15 distinct research communities that focus on methodology (I am not counting the myriad application domains). I came to call this the “jungle of stochastic optimization,” as this captured the diversity among the communities.
The 15 communities use eight distinct notational systems, in addition to various dialects. More subtle are the meanings associated with common terms such as “state variable,” “decision/action/control,” “transition function,” “policy,” “objective function,” and “model.” There are sharp differences in how each community writes down a problem. Some use a standard formalism to find the best policy while optimizing some metric. Others express a problem by directly writing down a method for making a decision (known as a policy). There are also significant differences in the handling of uncertainty (if present).
One of the major challenges of sequential decision problems is finding good methods for making decisions. So far I have found about 45 ways of expressing “method of making a decision” in the English language (feel free to contribute your own right here). I have settled on the word “policy” which is familiar both in every day English, but is also widely used by some of the academic communities that work in this space.
I present the modeling style of each of the 15 communities in chapter 2 of my new book, Reinforcement Learning and Stochastic Optimization: A unified framework for sequential decisions, (see section 2.1). This makes it possible for people to quickly review all the different modeling styles, since I use the notation of each community as well as the way each community expresses a problem on paper.
Just as important as the differences in how problems are expressed on a sheet of paper is the characteristics of the problems that each community tends to tackle. Not surprisingly, this is a moving target since the pressure to innovate pushes each community to search out new applications. Part of the language challenge is that the terms used by different communities (such as “control” in engineering or “action” in computer science) tends to come with preconceptions about the class of problems (engineers tend to work on continuous problems, computer scientists tend to work on problems with discrete actions).
In my book I offer a single modeling framework that represents any sequential decision problem. I argue that all the different methods for making decisions can be organized into four classes of policies (see Chapter 11 for a thorough discussion of all four classes, which are then covered in depth in chapters 12-19). I present a problem involving energy storage (in chapter 11) where I show that each of the four classes of policies may work best depending on the specific characteristics of the data. I also point out a number of ways to build hybrids involving two or more classes of policies (see section 11.7). This finding highlights the need to combine the skills of all of the communities!
As this is being written, several communities are steadily developing methods that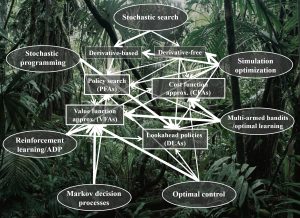
fall in each of the four classes of policies, increasing the overlap that otherwise remains hidden behind the fog of languages. I prepared the graphic to the left that illustrates how seven of the 15 communities have steadily evolved from one to up to four classes of policies (click here for a very short powerpoint presentation with this slide).
Designing a common language helps to expose the differences in the languages used by the different communities. At the same time, it highlights the benefits of a common language, since each community has contributed different methods for solving problems. However, there is a big gap between creating a common language, and having everyone speak it.
An even bigger challenge than bridging different methodological communities is reaching out to the myriad application domains, where the most important issues are 1) the accessibility of the mathematics, 2) the ability to represent the problems within a problem domain, and 3) the ability to offer practical, implementable tools that work for a problem class.