Warren B. Powell
Professor Emeritus, Princeton University
Chief Innovation Officer, Optimal Dynamics
The IC-VRP is a new class of stochastic vehicle routing problems where the vehicle (which could be a drone) collects information as it moves around, and where this information is used to make decisions that are implemented that change the physical system in some way.
My work in this rich new problem class began with two papers:
Lina al-Kanj, Warren Powell, Belgacem Bouzaiene-Ayari, The Information-Collecting Vehicle Routing Problem: Stochastic Optimization for Emergency Storm Response, Jan 17, 2023, https://tinyurl.com/ICVRPStorm/.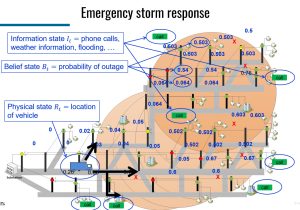 
This paper routes a single utility truck around a grid which is described by a physical state (e.g. its location), other information (e.g. lights-out calls), and belief states, which capture the probability that there is an outage on a segment of the network. Behind the scenes is the grid itself, which has a tree structure that allows us to make inferences about where a line might be down based on the lights-out calls. As the truck travels, it observes the presences of outages (information collection), and can stop and perform repairs (implementation). The paper uses a novel form of Monte Carlo tree search (called “optimistic MCTS”) that plans into the future, and is able to handle the very high-dimensional (and continuous) state vector (the belief state variable alone has hundreds of dimensions, consisting of continuous estimates of probabilities).
Lawrence Thul, W.B. Powell, An An Information-Collecting Drone Management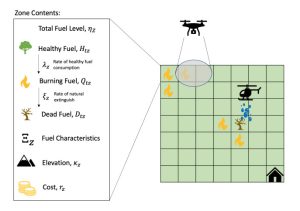
Problem for Wildfire Mitigation, Jan 18, 2023. https://tinyurl.com/ICVRPWildfire – This paper optimizes the movement of a drone that collects information about a rapidly moving wildfire, using a wildfire model from the literature. The drone needs to move to zones to observe the status of the wildfire (the “information collection” decision). This information is used to update beliefs about the wildfire, which is then communicated to a helicopter which then travels out and dumps fire retardant (the “implementation decision”). The research considered all four classes of policies, reporting on the performance of the two best. The best performance was a lookahead policy which captured the value of information, drawing on the principles behind the knowledge gradient.
There is an extensive literature on pure learning problems that often goes by the name “active learning” or, “multiarmed bandit problems.” Active learning/bandit problems arise when the information we observe depends on decisions that we make. For example, we may observe a patient’s response to a drug (which we choose) or how many clicks an ad receives (a popular problem in the tech sector).
For newcomers to the field, I strongly recommend Chapter 7 in my book Reinforcement Learning and Stochastic Optimization: A unified framework for sequential decisions. The chapter shows how to model active learning problems (the chapter is titled “Derivative-Free Stochastic Optimization” which is a more general term for this problem class), and illustrates all four classes of policies (see sections 7.3 – 7.7).
I have done a lot of work on pure learning problems using a lookahead policy introduced by Peter Frazier called the knowledge gradient. The most popular class of policies, widely used in the tech sector, are known as “upper confidence bounding.”
Introducing the dimension of a physical state when we have to route a vehicle to collect information completely changes the character of the problem. There is no shortage of research questions that arise in this new problem class:
- Learning arises in many settings, and each will have its own belief state (the model used to capture what is uncertain about the problem).
- MCTS is a very general purpose strategy, but it is computationally expensive. Are there ways to make it more efficient? The storm response paper used a form known as optimistic MCTS, which required solving sampled lookahead problems optimally. The more traditional (pessimistic) MCTS is computationally easier. These should be compared.
- Knowledge gradient (aka “value of information”) policies offers an alternative approach. These need to be tested and compared.
- Upper confidence bounding falls in the class of “parametric cost function approximations” (see also https://tinyurl.com/cfapolicy/). For active learning, these policies put a bonus on uncertainty which requires the design of a creative parameterization. Designing (and tuning) a CFA policy for active learning in the context of VRP is an open (and attractive) research area.
- Now extend any of these ideas to problems with fleets of vehicles, that make it possible to perform learning in parallel.
Physical states can arise in other contexts that involve learning. These problems might involve a wide array of inventory problems, supply chain problems, health applications and energy systems.
A closely related problem is the “exploration vs. exploitation” problem of approximate dynamic programming, where learning about the value of being in a (typically physical) state requires visiting the state, where we are learning about the value of being in the physical state.